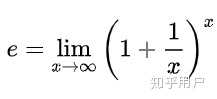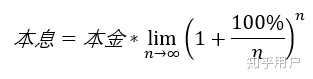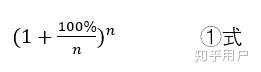一、这问题问的不对，这问题就好比在问圆周长除以直径为什么等于π了。哪里需要搬出高数教材？

二、常数e的定义计算式就是：

e的发现（对，是发现，不是发明）来自于雅各布·伯努利提出的银行复利问题：

如果银行的年复利是100%，那么一年后本息一共多少钱呢？

（分析：这取决于银行多长时间对你的本金核算一次。若一年核算一次本金，那一年后就得到2倍的钱。但是如果半年核算一次本金呢？三分之一年核算一次本金呢？……每天、每小时、每分钟核算一次本金呢？）一年内内核算本金次数记为n，列式如下：

所以，年复利100%，一年内核算无数次本金，一年后能得到的钱不是没有限制的，它接近于本金x一个常数，这个常数就是不断放大n来算啊算啊，等于2.71828 18284 59045 23536……,伟大的数学家欧拉把这个增长常数算出来并命名为e。

三、应用一瞥：

e在日常生活中有什么应用呢：感兴趣可以搜一下72法则（因为2约等于e的0.72次方），适合快速估算：如果银行给你的年复利是5%，那你本金翻倍的时间就是14.4年：72除以5。(由于72是近似值，所以存在误差问题，而超过三年，误差就非常非常小了，所以很好用)

e在高等数学中：在所有指数函数中，唯有y=e^x的导数和积分都等于它自己e^x

四、为什么叫自然常数呢：

e其实就是单位时间内，持续的翻倍增长所能达到的极限值。

比如：细胞分裂是一个细胞分裂为两个细胞，这就是翻倍增长（即取100%），那么就要问了：假如细胞连续分裂，分裂时长为一天，那么1个细胞在1天结束那刻是几个细胞了呢？

所以要算增长倍数。

粗糙的说，是2。

这其是假定两个细胞完全分开后才各自进行新的分裂（①式中n=1）

But! 如果不等细胞完全生成，即开始新的分裂呢？这才是自然真相：

二分之一天就开始新分裂（①式中n=2）

三分之一天就开始新分裂（①式中n=3）

四分之一天就开始新分裂（①式中n=4）

……

n分之一天就开始新分裂（①式中n=n）

将n取无穷大，那一天后就存在e个细胞。

这数就像自然定律一般存在，所以叫自然常数。